HOME

SoapTools

SoapTools is a Blender extension for 3D modeling based on constraint systems, encouraging formal emergence through the exploration of constraints rather than the definition of fixed problems with optimal solutions.

It also serves as a personal testbed for implementing and consolidating everything I’ve learned about geometry processing over the years.

All operations are implemented in PyTorch and are differentiable. Future releases will integrate differentiable rendering to support vision and GenAI based optimization paradigms such as Score Distillation Sampling. This extension is my way of creating artistic value out of all the research I’ve been exposed to in the last year or so. I want this to become a place where all the non-optimalities and quirks of publications of the past become valuable tools for creative expression.

CPU-only releases are available for download. For installation, refer to this guide. For running with CUDA enabled or to access the dev build, refer to the README.

Minimal Surfaces

I orginally started this project because I wanted a minimal surface solver for Blender. As such, SoapTools got its name from the very similar qualities to a minimal surface of soap bubbles sttached to different objects. SoapTools provides an operator to generate minimal surfaces of a mesh with pinned constraints.

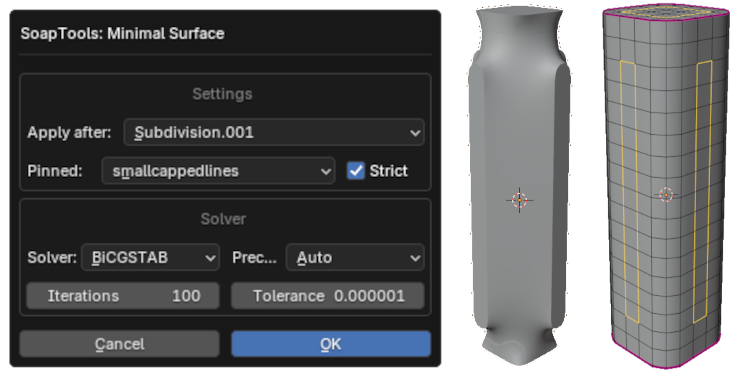A minimal surface derived from the the mesh to its right, with the pinned areas in yellow.

Maps

Maps form the basis of specification for constraints. Anything that specifies values over a mesh can be used as a map.

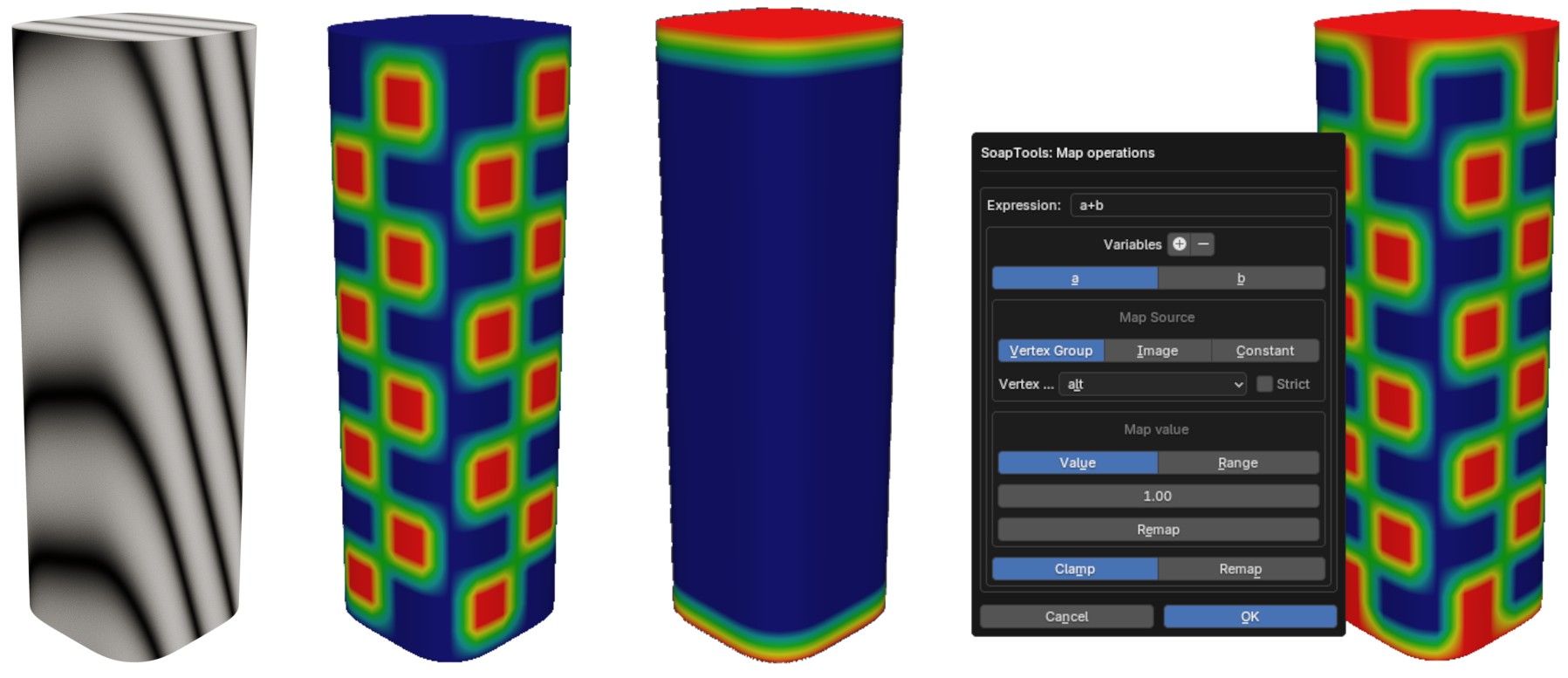Shader ouput can also be used as maps, with built-in tools provided for baking channels and per-vertex sampling from the baked image (left). Alternatively, Simple vertex groups can also be used (middle). Mathematical operations can also e defined to combine different maps, using a dedicated symbolic parser (right).

Flation

It isn’t exactly displacement nor in/deflation, so its name for now is flation. This is the current main operator for form generation in SoapTools. It essentially solves a constraint system based on 4 specific penalties, all user-definable through maps:

  • Displacement: This constraint specifies the target displacement distance of a vertex, but not the direction.
  • Smoothness: This constraint is derived from the Laplacian of the output mesh. Positive values for this constraint encourage locally smooth surfaces, while negative values yield more curvature, which usually manifests as wrinkles.
  • Normal: This constraint maintains freedom of movement of vertices, but encourages the norm of the output displacement onto the veretx’s normal vector to match target displacement.
  • Tangent: This constraint is essentially the opposite of the normal constraint. Higher values enforce the displacement vector to align closer to the vertex’s normal vector.

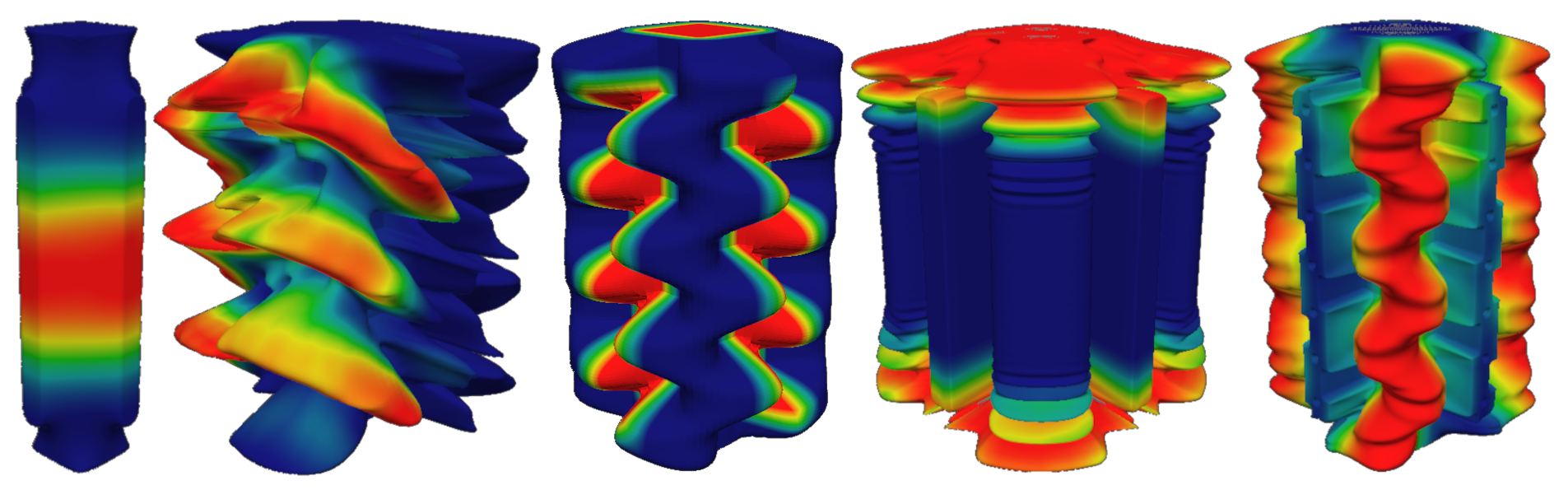
Different constraint systems defined over the same base mesh (left) can yield very different results.

Interpolation

While results from the flation operator may be interesting, it is quite hard to have an intuition for the output of a system with so many moving parts. The interpolation operator enables the user to interpolate between multiple shapes based on weights attributed by their respective maps.
Results from the flation operator can be considered to be a swatch of shapes from which the user can choose which moments are worth keeping.

Interpolation weights are mapped onto individual meshes (in this case simply painted on), specifying which parts should be kept.

Extremely different results can be found by exploring the interpolation space.